File:Gradient descent.gif
From KYNNpedia
Gradient_descent.gif (360 × 292 pixels, file size: 1.51 MB, MIME type: image/gif, looped, 50 frames)
This file is from Wikimedia Commons and may be used by other projects. The description on its file description page there is shown below.
Summary
| DescriptionGradient descent.gif |
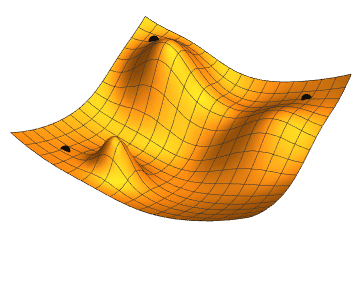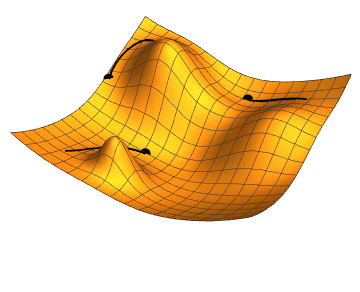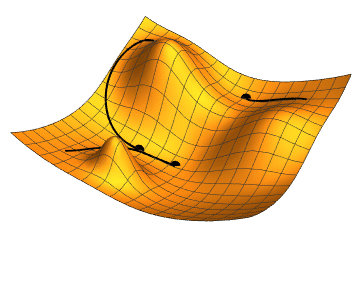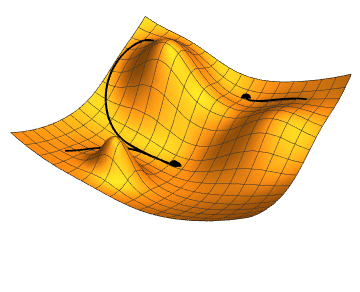
English: Gradient descent is a simple method to find the minimum of a function, where at each iteration a small step is made in the direction of the steepest descent. It tends to get stuck in a local minimum, so it is often run with several initial conditions. |
| Date | |
| Source | https://twitter.com/j_bertolotti/status/1121054414066810881 |
| Author | Jacopo Bertolotti |
| Permission (Reusing this file) |
https://twitter.com/j_bertolotti/status/1030470604418428929 |
Mathematica 11.0 code
f = Evaluate[x^2 + y^2 + Total@Table[RandomReal[{0,2}] E^(-(((x - RandomReal[{-1, 1}])^2 + (y + RandomReal[{-1, 1}])^2)/(2 RandomReal[{0.1, 0.4}]^2))), {10}]];
step = 0.02;
nstep = 100;
coord = {-1, 1};
pos = {coord[[1]], coord[[2]], f /. {x -> coord[[1]], y -> coord[[2]]}};
evo = Reap[Do[
subst = MapThread[Rule, {{x, y, z}, pos}];
dfx = (D[{x, y, f}, x] /. subst);
dfy = (D[{x, y, f}, y] /. subst);
tmp = {D[f, x] /. subst, D[f, y] /. subst};
pos = pos - step {tmp[[1]], tmp[[2]], 0};
pos[[3]] = Evaluate[f /. {x -> pos[[1]], y -> pos[[2]]}];
Sow[pos];
, nstep];][[2, 1]];
coord = {-1, -1};
pos = {coord[[1]], coord[[2]], f /. {x -> coord[[1]], y -> coord[[2]]}};
evo1 = Reap[Do[
subst = MapThread[Rule, {{x, y, z}, pos}];
dfx = (D[{x, y, f}, x] /. subst);
dfy = (D[{x, y, f}, y] /. subst);
tmp = {D[f, x] /. subst, D[f, y] /. subst};
pos = pos - step {tmp[[1]], tmp[[2]], 0};
pos[[3]] = Evaluate[f /. {x -> pos[[1]], y -> pos[[2]]}];
Sow[pos];
, nstep];][[2, 1]];
coord = {1, 1};
pos = {coord[[1]], coord[[2]], f /. {x -> coord[[1]], y -> coord[[2]]}};
evo2 = Reap[Do[
subst = MapThread[Rule, {{x, y, z}, pos}];
dfx = (D[{x, y, f}, x] /. subst);
dfy = (D[{x, y, f}, y] /. subst);
tmp = {D[f, x] /. subst, D[f, y] /. subst};
pos = pos - step {tmp[[1]], tmp[[2]], 0};
pos[[3]] = Evaluate[f /. {x -> pos[[1]], y -> pos[[2]]}];
Sow[pos];
, nstep];][[2, 1]];
p1 = Table[
Show[
Plot3D[f, {x, -1.35, 1.35}, {y, -1.35, 1.35}, Boxed -> False, Axes -> False(*,PlotStyle\[Rule]{Opacity[0.3]}*)],
Graphics3D[{PointSize[0.03], Point[evo[[j]] ], Thick, Line[evo[[1 ;; j]] ], Point[evo1[[j]] ], Line[evo1[[1 ;; j]]] , Point[evo2[[j]] ], Line[evo2[[1 ;; j]]] }]
]
, {j, 1, nstep, 2}];
ListAnimate[p1]
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
| This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. | |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
Captions
Gradient descent with 3 different initial conditions.
Gradient descent with 3 different initial conditions.
Items portrayed in this file
depicts
some value
24 April 2019
image/gif
1,586,553 byte
292 pixel
360 pixel
5f21ecb37864995659c598e1bd301e90e17ae8b1
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 08:43, 25 April 2019 |  | 360 × 292 (1.51 MB) | wikimediacommons>Berto | User created page with UploadWizard |
File usage
The following page uses this file:
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| GIF file comment | Created with the Wolfram Language : www.wolfram.com |
|---|