File:DipoleContourPoint.svg
From KYNNpedia

Size of this PNG preview of this SVG file: 558 × 449 pixels. Other resolutions: 298 × 240 pixels | 597 × 480 pixels | 955 × 768 pixels | 1,273 × 1,024 pixels | 2,545 × 2,048 pixels.
Original file (SVG file, nominally 558 × 449 pixels, file size: 94 KB)
This file is from Wikimedia Commons and may be used by other projects. The description on its file description page there is shown below.
Summary
| DescriptionDipoleContourPoint.svg |
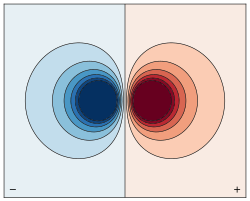
English: Contour plot of the equipotential surfaces of the electric field of a point-like dipole. The field is accurately computed from a physical model. The dipole points in x-direction  . . |
| Date | |
| Source | Own work |
| Author | Geek3 |
| Other versions |
 |
| SVG development InfoField | |
| Source code InfoField | Python codeimport numpy as np
from matplotlib import pyplot as plt
from matplotlib import colors
def simplify_contours(qcset, thresh=plt.rcParams['path.simplify_threshold']):
for c in qcset.collections:
paths = c.get_paths()
for i, p in enumerate(paths):
p.simplify_threshold = thresh / plt.gcf().dpi
paths[i] = p.cleaned(simplify=True)
# dipole in x-direction
p = np.array([1., 0.])
xmax = 2.5
ymax = 2.0
vmax = 0.18
ngrid = 400
levels = np.linspace(-vmax, vmax, 23)
X, Y = np.mgrid[-xmax:xmax:ngrid*1j, -ymax:ymax:int(ngrid*ymax/xmax)*1j]
# formula for dipole potential https://en.wikipedia.org/wiki/Dipole#Field_from_an_electric_dipole
V = np.dstack((X, Y)).dot(p) / (4. * np.pi * np.hypot(X, Y)**3)
V = np.clip(V, -2.*vmax, 2.*vmax)
plt.figure(figsize=(6, 6 * ymax / xmax)).add_axes([0, 0, 1, 1])
contf = plt.contourf(X, Y, V, levels=levels, cmap='RdBu_r', extend='both',
norm=colors.SymLogNorm(linthresh=0.5*vmax, vmin=-vmax, vmax=vmax))
simplify_contours(contf, 0.8*plt.rcParams['lines.linewidth'])
cont = plt.contour(X, Y, V, levels=contf.levels, colors='k', linestyles='solid')
plt.xticks([]), plt.yticks([])
plt.gca().set_aspect(aspect='equal')
for i in -1,1:
plt.text(0.15*i, 0, {-1:u'\u2212', 1:'+'}[i], size=18, ha='center', va='center')
plt.savefig('DipoleContourPoint.svg', bbox_inches='tight', transparent=True,
edgecolor='none')
|
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
This file is licensed under the Creative Commons Attribution-Share Alike 4.0 International license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Captions
Add a one-line explanation of what this file represents
Items portrayed in this file
depicts
8 September 2019
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 09:59, 8 September 2019 |  | 558 × 449 (94 KB) | wikimediacommons>Geek3 | User created page with UploadWizard |
File usage
The following page uses this file:
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| Width | 446pt |
|---|---|
| Height | 359pt |